Superposition Theorem

    

     Superposition theorem is one of those strokes of genius that takes a complex subject and simplifies it in a way that makes perfect sense. A theorem like Millman's certainly works well, but it is not quite obvious why it works so well. Superposition, on the other hand, is obvious.

     

     The strategy used in the Superposition Theorem is to eliminate all but one source of power within a network at a time, using series/parallel analysis to determine voltage drops (and/or currents) within the modified network for each power source separately. Then, once voltage drops and/or currents have been determined for each power source working separately, the values are all “superimposed” on top of each other (added algebraically) to find the actual voltage drops/currents with all sources active.

Steps in Superposition Theorem

1. Turn off all independent sources except one source. Find the output (voltage or current) due to that active source using nodal or mesh analysis.
2. Repeat step 1 for each of the other independent sources.
3. Find the total contribution by adding algebraically all the contributions due to the independent sources

 

To calculate the contribution of each source independently, all the other sources must be removed and replaced without affecting the final result.

When removing a voltage source, its voltage must be set to zero, which is equivalent to replacing the voltage source with a short circuit.

When removing a current source, its current must be set to zero, which is equivalent to replacing the current source with an open circuit.

 

Now let's explore an example.

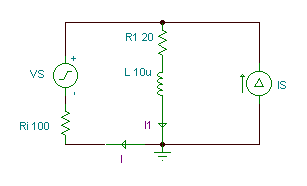
In the circuit shown below,

 

R_i = 100 ohm, R₁ = 20 ohm, R₂ = 12 ohm, L = 10 uH, 
C = 0.3 nF, v_S(t)=50cos(wt) V, i_S(t)=1cos(wt+30°) A,  
f=400 kHz. 

  

First substitute an open circuit for the current source and calculate the complex phasors I', I1' due to the contribution only from VS.

The currents in this case are equal:

I' = I₁' = V_S/(R_i + R₁ + j*w*L) 

= 50/(120+j2*p*4*10⁵*10^-5) 

= 0.3992-j0.0836

I' = 0.408 e^{j 11.83°} A 

 Next substitute a short-circuit for the voltage source and calculate the complex phasors I'', I1'' due to the contribution only from IS.

In this case we can use the current division formula: 

I'' = -0.091 - j 0.246 A 

and 

I₁^" = 0.7749 + j 0.2545 A 

The sum of the two steps:

I = I' + I" = 0.3082 - j 0.3286 = 0.451 e^{- j 46.9°} A

I₁ = I₁^" + I₁' = 1.174 + j 0.1709 = 1.1865 e^{j 8.28°} A 

The time functions of the currents:

i(t) = 0.451 cos (w×t - 46.9°) A

i₁(t) = 1.1865 cos (w×t + 8.3°) A